124 125 (3)

124 **r*rx''*WMŁS Przestrzenie euklidesowe
a) Mimy (t’i > Va) - 0, | tj | = \/20, | i.*21 = y/45. Jest to więc baza ortogonalna przestrzeni E*. a współrzędne [oi, a?] wektora u w lej bazie wyrażają się wzorami
|vi|2
A. — _ _ (**» *3) _ 12 _ 4
20 ID’ ~ |v212 - 45 “ Ts
b) Zachodzą związki (5X, 63) = (*,, *3) = (t52: v3) = 0. Ponadto |v,| = \ v2 \ = | £31 = 1
Rozważana baza jest zatem ortonormalna Współrzędne (^i, wektora ti w tej bazie
są równe
(i, Ł'i ) = 0 02 = (ti 1 i^) —
03
= («, tJ3) = -2%/i
V 3- =
c) Łatwo się przekonać, że
(Pi>Pz) = (Pi.Pa) = (Pi.P<) =(Pa P3) = (P2.P«) = (P3.P4) = °
Dalej
IpiI = 2, |p2| = |p3| = i, |pĄ\ =3.
Stąd wynika, że podana baza jest ortogonalna, a współrzędne (yi, 72 73, 74] wektora q w Lej bazie są równe
= tg. p.> = 1 _ i _ (<?,?,) _ -3 _
n . .2 « “ o» 72 — — ~r~ — — —o,
Ip2|
73
= P3) = l = O ~ = P«) _ 0
ip3r 1 * 4 iP4r *
Sprawdzimy jeszcze, ze rzeczywiście x2 - x + 1 = i • 2 - 3 (r — r2) + 2 fz + 2z2) .
• Przykład 13.2
j~2 [2 (~2
Sprawdzić, że funkcje y — sin 2ar, y — $in4z. y — sinor, ... twrorzą nieskończony układ ortonormalny w przestrzeni euklidesowej wszystkich rzeczywistych funkcji ciągłych na przedziale [— — J z iloczynem skalarnym określonym wzorem
a
(/,!?) = J Ąt)g(x)dz.
Rozwiązanie
Obliczmy najpierw normy wszystkich podanych funkcji Dla n € N mamy
*
=(H)i =
V -t /
sin 2nx
/7.
1.
Tizynasty tydzień - przykłady
ićb
Ortogonalność wszystkich par funkcji z podanego zbioru wynika z tego, ze dla dowolnych m,n £ A' takich, że n rn zachodzi zależność
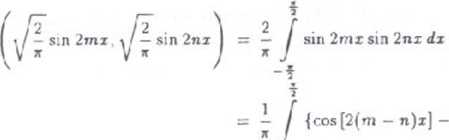
cos [2(m + n)z]} fiz
-ł
|
[sin [2(m - n)r] |
i |
sin [2(m 4 n}r] |
|
2x(m - n) |
r “7 |
2ar(m 4 n) |
= (0 - 0) - (0 - 0) = 0.
Uzyskane wyniki potwierdzają więc ortonorir.alność danego zbioru funkcji.
• Przykład 13.3
Stosując metodę Grama Schmidta zortogonalizować podane wektory zc wskaza nych przestrzeni euklidesowych:
a) Sj = (1, -2,0), U2 = (5, 5,1), u3 = (5,4,4) w przestrzeni E'\
b) ii i = (1,0,1,0). tt2 — (0,2,2,0), U3 = (0,1,0 1) w przestrzeni EA\
c) p, = 1, p2 x, p3 = z2 w przestrzeni i?2[^] z iloczynem skalarnym określonym wzorem
(p. <i) = p(-i)^(-i) + P(0)«(0) + p0)?U)
Rozwiązanie
OrtogonaJizacja Grarna Schmidta liniowo niezależnych wektorów iii, u2. . u„ w przestrzeni euklidesowej E polega na wyznaczeniu takich wektorów ortogonalnych tja, v2} . ., vn, aby układy wektorów {, £2, -.., Uk) eraz {vy, ?2, • • •, &’*} generowały te same przestrzenie dla k = 1,2,... n.
a) Dokonamy bezpośredniej konstrukcji wektorów th, v2t metodą Grama-Schmidta. Przyjmijmy na początku, że 3] = 5} = (1,—2,0). Warunek generowania identycznych przestrzeń: przez wektory ii] i {i; jest oczywiście spełniony. Równość
lin { ui. i2} = lin { Vj, v2 }
będzie zagwarantowana, gdy wektor v2 będzie postaci
v2 — u 2 4- a t5j = (5 + d 5 — 2a, 1), gdzie a £ R.
Współczynnik a obliczamy z warunku ortogonalności v2 -L V\. Mamy
(«i, %) = (5 + a) • 1 + (5 - 2«) - (-2) + 1 0 = -5 + 5a = 0.
Stąd a = 1 i v2 = (6,3, 1). Wektor £3 wyznaczamy z warunku
V3 = U3 + bvi -t- c v2 — (5 + b 4 6c, 4 — 26 4- 3c, 4 -f c), gdzie b,c £ R,
Wyszukiwarka
Podobne podstrony:
124 125 (3) 124Przestrzenie euklidesowe a) Mamy (t i, $3) = 0,
12451 P8022917 59 l 125 2 S 10 11 12 13 14 15 10 17 18 19 20 21 22 23 3 lUwigma
DSC00154 (21) •2 i jest to: ittrza w wentylowanej przestrzeni^ zastosowaniem nawiewników i wywiewnik
page0134 124 cznych zjawisk, i przestawszy hyć sam cudemr przyczyni się do wyjaśnienia jaki nam
DSC07353 124 Geometria analityczna w przestrzeni Przechodzimy teraz do równania parametrycznego plaa
116 117 (4) 116 Przestrzenie euklidcsowe 3. (aź, y) = 3 (azij y; - 2(crn ) y2 - 2(q X2}»i +4 {orz2)y
118 119 (4) - -Przestrzenie euklidesowe MU • — * a) (P.«) = p(-1)9(-1) + P(2)ł(2);
132 133 (3) 132 Przestrzenie euklidesowwę f) / = ł w przestrzeni lin {1 ,sin z, si
Rachunek różniczkowy odwzorowań określonych i o wartościach w przestrzeniach euklidesowych. Pochodne
118 119 (4) 118 Przestrzenie euklidesowo a) (P. Q) = P(-l)d(-l)
120 121 (3) 120 37f HlufliTfflą SSjSrrtiTr*ńi Przestrzenie euklidesowe Zatem cos iaz + 6,sin z
130 131 (3) 130 Przestrzenie euklidesowe b) Niech {ej. 52,^3, e^} będzie bazą standardową przestrzen
134 135 (3) 134 Przestrzenie euklidesowoOdpowiedzi i wskazówki 13.1 a) d) 231 / —V 10 V 10 ; e) [5,2
Zajmiemy się wyłącznie przestrzenią euklidesową, opisaną za pomocą współrzędnych
więcej podobnych podstron