Interpretacja geometryczna pochodnej

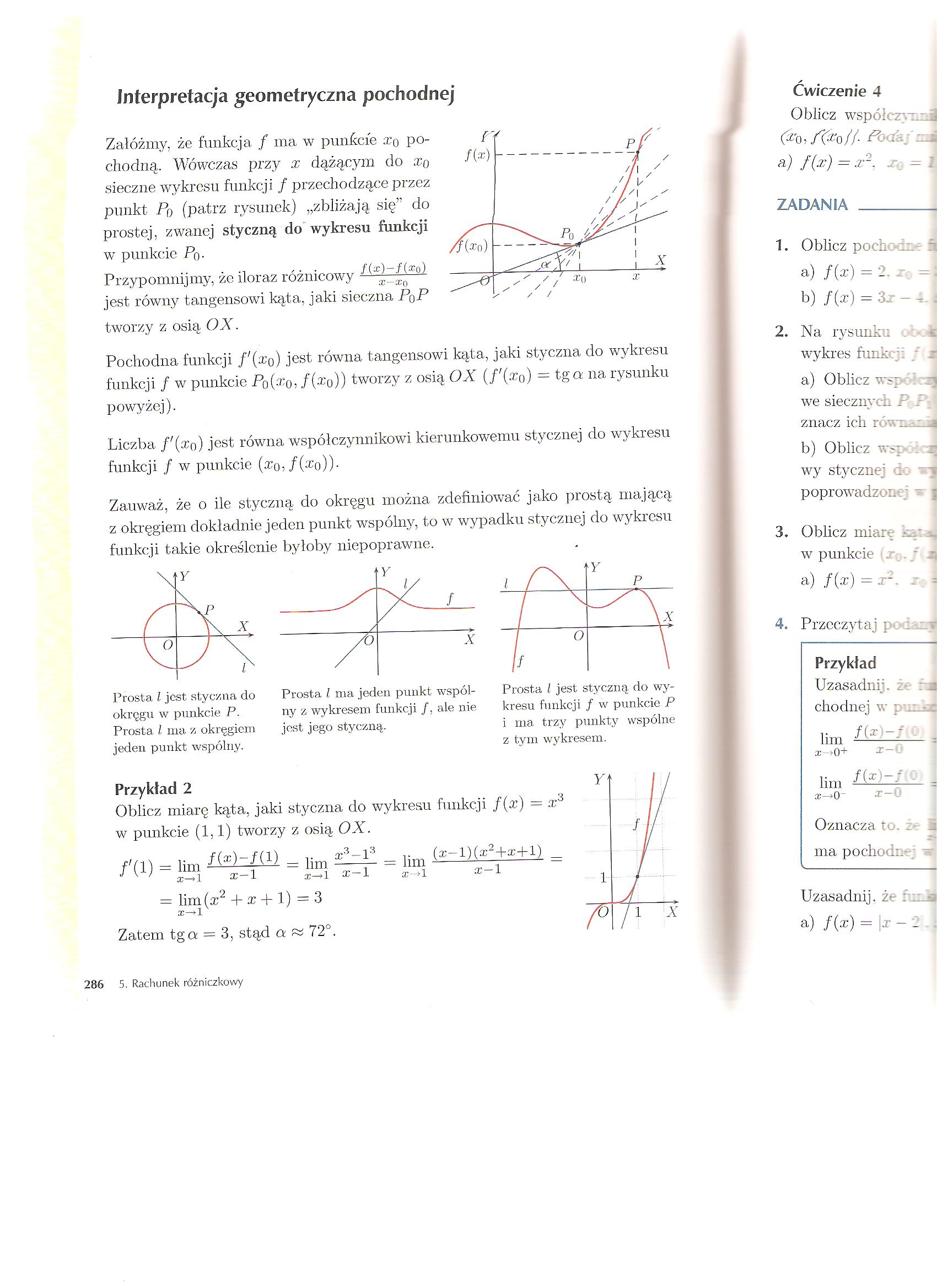
Załóżmy, że funkcja / ma w punkcie xq pochodną,. Wówczas przy x dążącym do xq sieczne wykresu funkcji / przechodzące przez punkt Pq (patrz rysunek) „zbliżają się” do prostej, zwanej styczną do wykresu funkcji w punkcie Pq.

Przypomnijmy, żc iloraz różnicowy ^ jest równy tangensowi kąta, jaki sieczna PqP tworzy z osią OJ.

Pochodna funkcji f'(xo) jest równa tangensowi kąta, jaki styczna do wykresu funkcji / w punkcie Pq (xq , f(x o)) tworzy z osią OX (/'(.£ o) — tg a na rysunku powyżej).

Liczba f(xo) jest równa współczynnikowi kierunkowemu stycznej do wykresu funkcji / w punkcie (^₀,/(^o))-

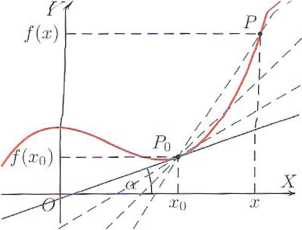
Zauważ, że o ile styczną do okręgu można zdefiniować jako prostą mającą z okręgiem dokładnie jeden punkt wspólny, to w wypadku stycznej do wykresu funkcji takie określenie byłoby niepoprawne.

Prosta l jest, styczna do okręgu w punkcie P. Prosta. I ma. z okręgiem jeden punkt wspólny.

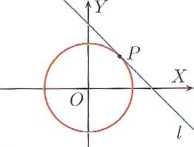
Prosta l ma jeden punkt wspólny z wykresem funkcji /, ale nie. jest jego styczną.

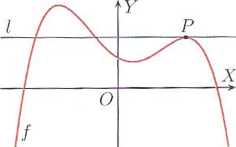
Prosta l jest styczną do wykresu funkcji / w punkcie P i ma trzy punkty wspólne z tym wykresem.

Przykład 2

Oblicz miarę kąta, jaki styczna do wykresi w punkcie (1,1) tworzy z osią OX.

f'( 1) = - lim    — Hm ——- lim

' ^v ' x—x-l    _x—* i x-l _x >1

= lim (x² -f x + 1) = 3

X—>1

Zatem tg a = 3, stąd a ~ 72°.

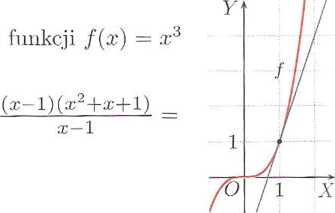
Ćwiczenie 4

Oblicz współcz

(Po,    ' Z_I

a) f(x) = x². . ZADANIA _

1.    Oblicz poci:

a)    f(x) = i.

b)    f{x) = 3-r

2.    Na rysunku wykres funk

a.) Oblicz vo: we siecznych F znacz ich równam*

b) Oblicz ”.>t wy stycznej poprowadzeń

3.    Oblicz miarę -w punkcie

a) f{x) = P.

4.    Przeczytaj p. i -

Przykład

Uzasadnij, z chodnej w -

lim -^jC(“    -

x- >0+

lim    ~- =

x_>o    x-

Oznacża te. z ma pochodu-'

v____

Uzasadnij, że :

^a) f(%) = x - _

286    5. Rachunek różniczkowy