1 (48) 3

3. Ciągi i szeregi liczbowe

3.24.    TWIERDZENIE. Szereg o wyrazach nieujemnych (*) jest zbieżny wtedy i tylko wtedy, gdy jego sumy częściowe tworzą ciąg ograniczony.

Przejdziemy teraz do cech zbieżności innego rodzaju, do tak zwanego kryterium porowa nawczego.

3.25.    Twierdzenie, a) Jeśli \a„\ < c„ dla n > N₀, gdzie N₀ jest pewną ustaloną liczba

całkowitą, i jeśli szereg %c_Kjest zbieżny, to i szereg    „ jest zbieżny.

b) Jeśli a_B > d_H> Odlan > N₀ i jeśli Y,d_Kjest rozbieżny, to i szereg %a_njest rozbieżnyą

Zauważmy, że b) odnosi się tylko do szeregów o wyrazach nieujemnych a„.

Dowód. Weźmy e >0, wówczas istnieje N > N₀ takie, że m > n > JV implikuje £    <1

<e, co wynika z kryterium Catichy’ego. Stąd

i a) zostało udowodnione.

Dalej, b) wynika z a), dlatego, że jeśli szereg £a„ jest zbieżny, to i szereg musi być zbieżny (zauważmy, że b) wynika także z twierdzenia 3.24).

Kryterium porównawcze jest bardzo użyteczne; aby można było skutecznie je stosować, musimy zaznajomić się z pewną ilością szeregów o ujemnych wyrazach, wiedząc z góry, czy są zbieżne, czy nie.

Szeregi o wyrazach nieujemnych

Najprostszym z takich szeregów jest być może szereg geometryczny. 3.26. Twierdzenie. Jeśli O ^ x < 1, to

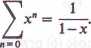
Jeśli x^l,to ten szereg jest rozbieżny. Dowód. Jeśli x # 1, to

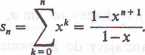
Przy n dążącym do oo otrzymujemy żądany wynik. Dla x = 1 otrzymujemy szereg l+ł% + 1+..., który oczywiście jest rozbieżny.

(‘) Wyrażenie „nieujemny" będzie się odnosiło wszędzie do liczb rzeczywistych.

Wyszukiwarka

Podobne podstrony:
43 9 Twierdzenie 3. Szereg o wyrazach nieujenmych jest zbieżny wtedy i tylko wtedy, gdy jego ciąg su
Szeregi o wyrazach nieujemnych Twierdzenie 8. Szereg o wyrazach nieujemnych jest zbieżnym wtedy i ty
Kryterium cTAIemberta Twierdzenie 11 (Kryterium d’Alemberta zbieżności szeregu o wyrazach nieujemnyc
4.1 Szeregi o wyrazach dodatnich Ciąg sum częściowych szeregu o wyrazach dodatnich jest ciągiem rosn
10 (72) 223 Formy różniczkowe 10.24. TWIERDZENIE. Załóżmy, że co jest k-formą na pewnym zbiorze otwa
MATEMATYKA035 m. 62 U Ciągi i szeregi liczbowe Z tej ostatniej nierówności i twierdzenia o granicy t
MATEMATYKA041 74 II. Ciągi i szeregi liczbowe Ponieważ twierdzenia proste i przeciwstawne są równowa
8 (1176) 62 Rozdział 4- Ciągi i szeregi 4- 1. Ciągi liczbowe i ich g Przykład 4.22. Aby zilustr
4 (1737) 58 Rozdział 4- Ciągi i szeregi Ą.l. Ciągi liczbowe i ich granU Twierdzenie 4.10. Grani
MATEMATYKA045 82 D. Ciągi i szeregi liczbowe TWIERDZENIE 2.5 Jeżeli szereg XlaJ jest zbieżny, to sze
skanuj0009 (302) j.2. Szeregi liczbowe 71 Będziemy teraz rozważać szeregi o wyrazach dowolnych. OC D

więcej podobnych podstron