294 295

294 Programowanie wypukłe i kwadratowe

Rysunek 6.5

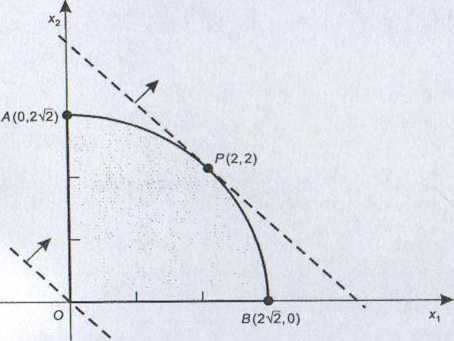
kierunku wzrostu funkcji celu określamy punkt P(2, 2) styczności warstwicy o najwyższej wartości funkcji celu ze zbiorem rozwiązań dopuszczalnych (rys. 6.5).

Przykład 6.2¹

Rozpatrujemy zadanie:

/(.jc,, x₂) = \Ox_i+25x₂-\Ox*-x₂-4x_ix₂ —» max, jc, + 2x₂ < 10,

Xi + x₂^9,

> 0,

x₂ Ss 0.

Funkcja celu jest funkcją kwadratową, a wszystkie warunki ograniczające są liniowe. Zadanie to można zapisać w postaci:

/(x) = p^Tx-x^TCx —» max,

Ax < b, (6-4)

x > 0,

przy czym:

10		10 2		1 2		10		*1
	- C =		, A =		, b =		, x =
25		2 1		1 1		9		*2

¹ Przykład został zaczerpnięty z książki W. Grabowskiego, Programowanie matematyczne, PWE, Warszawa 1980.

Macierz C jest dodatnio określona, czyli /(x) = p^Tx — x^TCx jest funkcją wklęsłą. Podobnie wszystkie warunki ograniczające jako funkcje liniowe są również wklęsłe. Jest to więc kolejny przykład zadania programowania wypukłego.

Zadanie postaci (6.4), w którym macierz C jest nieujemnie określona, nazywamy zadaniem programowania kwadratowego.

6.2.3. Warunki Kuhna-Tuckera

Z każdym zadaniem programowania nieliniowego można związać funkcję Lagrange’a, łączącą funkcję celu z ograniczeniami. Definiujemy ją następująco:

Z.(x, y)=/(x)+yg(x),

gdzie y jest elementem przestrzeni R"' i ma postać: y=[>’i, >’J-

Uwzględniając wszystkie składowe wektorów x oraz y, funkcję Lagrange’a można zapisać następująco:

L(X|, .... X„, >>,, ..., y„)=f(x_l> ..., x„)+ X y,gi(x......x„).

i= I

Jeżeli f oraz g< dla i= 1, ..., m mają pochodne cząstkowe, wówczas można skonstruować problem Kulma—Tuckera. Jest on złożony z czterech następujących warunków:

• warunek 1:

V,L(x, y) = 0,

gdzie symbol V,L(x, y) oznacza gradient funkcji L ze względu na zmienne tworzące wektor x, czyli:

V,L(x, y) =

d^x, y)

dx_n

• warunek 2: yg(x) = 0,

• warunek 3:

S(x)>0,

• warunek 4: