CCF03252008�009

r
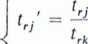
hj' = t,j - tik trj' (i * r, j = 0,1.....n).
(2.53)
Przekształcając elementy tablicy T według podanych wzorów, otrzymujemy w nowej tablicy T wektory jednostkowe dla nowego zestawu zmiennych bazowych.
Degeneracja rozwiązania bazowego. Możemy się zetknąć z tym problemem, gdy chociaż jedna zmienna bazowa jest zerowa. Wówczas mogą wystąpić tzw. martwe kroki, to znaczy przechodzimy od jednego rozwiązania bazowego do drugiego, związanego z tym samym punktem. Wartości zmiennych nie ulegają w tym przypadku zmianie, podobnie jak wartość funkcji celu. Teoretycznie możliwe jest powstanie cyklu, czyli ciągu rozwiązań, który będzie się stale powtarzał. Na szczęście w praktyce degeneracja rozwiązania bazowego albo znika, albo kolejne rozwiązanie zdegenerowane okazuje się rozwiązaniem optymalnym.
PRZYKŁAD 2.10
Rozwiążmy zadanie PL analizowane już wcześniej:
r
3*! + x2 -> max,
< 2xt + 3x, ^ 12,

(2.54)
Wprowadzając zmienne swobodne x3 i x4, sprowadzamy zadanie (2.54) do równoważnej postaci kanonicznej:
r
3xj + x2 + 0x3 + 0x4 -» max, 2x( + 3x2 + x3 + 0x4 = 12, 2.Xj -(- 0x2 + 0x3 + x4 — 6,
Xj, x2, x3, X4 5: 0.
(2.55)
Postać kanoniczna (2.55) jest zarazem postacią bazową, generującą początkowe, dopuszczalne rozwiązanie bazowe. Jeżeli zmiennymi bazowymi będą zmienne swobodne x3 i x4 z wektorami jednostkowymi:
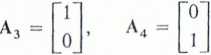
to z układu równań (2.55) można łatwo uzyskać początkowe rozwiązanie bazowe X1:
Xi = x2 = 0, x3 = 12, x4 = 6.
Wyjściowej postaci bazowej (2.55) odpowiada początkowa tablica simpleksowa T1 (tablica 2.5):
Tablica 2.5
|
Cj |
3 |
A |
0 |
0 |
v | |
|
Ci |
zmienna bazowa |
X2 |
Aj |
a4 | ||
|
0 |
Aj |
2 |
3 |
1 |
0 |
12 |
|
0 |
*4 |
fjn |
0 |
0 |
1 |
6 |
|
Zj |
0 |
0 |
0 |
0 |
*01 | |
|
[Oj |
3 |
t |
0 |
0 |
0 | |
Z tablicy simpleksowej T1 odczytujemy rozwiązania bazowe X1; pamiętamy, że zmienne niebazowe są zerowe: -W = x2 = 0 oraz że wartości zmiennych bazowych otrzymujemy z kolumny b;*:
A-3 = 12, X4 = 6, X0 = Cgg — 0.
Aby sprawdzić, czy rozwiązanie X1 jest optymalne, najpierw obliczamy parametry:
zj = Z c,t,j,
ieZB
a następnie wskaźniki kryterium optymalności t0j = Cj — r..
Rozwiązanie X1 nie jest optymalne, gdyż f01 = 3, f02 = 2 są dodatnie, a zadanie jest na maksimum. Zmienną wprowadzoną do bazy będzie zmienna x„ a zmienną usuwaną z bazy będzie zmienna x4, gdyż 6/2 < 12/2. Element t2l — 2 jest elementem centralnym przekształcenia simpleksowego. Nową postać bazową zawiera tablica 2.6.
Tablica 2.6
|
CJ |
3 |
3 |
0 |
0 | ||
|
zmienna bazowa |
A'i |
x2 |
X3 |
a4 | ||
|
0 |
Aj |
0 |
' 3 j |
i |
-1 |
6 |
|
3 |
Al |
1 |
0 |
0 |
1/2 |
3 |
|
Zj |
3 |
0 |
0 |
3/2 |
A01 | |
|
l0 i |
0 |
ą |
0 |
-3/2 |
9 | |
Elementy tablicy simpleksowej T2 uzyskujemy na podstawie (2.53). Najpierw ustalamy elementy wiersza centralnego, a następnie elementy po-
43
Wyszukiwarka
Podobne podstrony:
element regularny ▲ element rzeczywisty X Przekształcenie elementów regularnych w ich
P3213725 INNE PRZESTRZENIE NIEOGRZEWANE Ru Af całkowite pole powierzchni wszystkich elementów między
OPERACJE ELEMENTARNE I RZĄD MACIERZY Przekształceniami elementarnymi danej macierzy A=[^j]mxn nazywa
Rachunkowość jako baza informacyjna controllingu 53 Z wymienionych elementów sprawozdania „pro forma
DSC01407 1. Czy wykonując na układzie wektorów (A) przekształcenia elementarne a i (3 zmieniamy wekt
IMAG0982 Wybrane wartości kategorii zmęczeniowej Aac wg PN-90/B-03200 [53] Opis elementu
Matematyka 2 53 352 V. Elementy rachunku prawdopodobieństwu 352 V. Elementy rachunku prawdopodobień
mechanika0001 2 19. Podać definicję przekształceń elementarnych i twierdzenia ich
mechanika0001 2 19. Podać definicję przekształceń elementarnych i twierdzenia ich
img020 (49) 24 ków o wektor kolumnowy b wyrazów wolnych. Realizacja ciągu przekształceń elementarnyc
P2 19. Podać definicję przekształceń elementarnych i twierdzenia ich dotyczące, f/j) 20. Podać defin
DSC01407 (11) H 1. Czy wykonując na układzie wektorów (A) przekształcenia elementarne a i P zmieniam
więcej podobnych podstron