Matematyka 2 73

372 V. Elementy rachunku prawdopodobieństwu

ZL U o rozkładzie normalnym z wartością oczekiwaną p = 0 i odchyleniem standardowym o = 1 nazywa się zmienną losową o standaryzowanym rozkładzie normulinm N(0,1). Jej GP, którą będziemy oznaczać literą . jest więc postaci:

-ce<u<oc.

(6.7) <p(u)=-J=«e

V2it

Krzywa gęstości ZL o rozkładzie N(0.l) i związane z nią wartości niektórych czaraktcrystycznych pr-stw są pokazane na rysunku 6.4

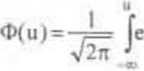
J.|3

² dt

Istnieją tablice wartości GP (p i odpowiadającej jej dystrybuanty O

(6.8)

oraz tablice kwanty Ii, tj liczb u_r spełniających warunek

-j=Jc ^: dl = p, czyli <P(u_r) = p.

-<o

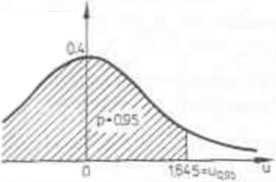
Tablice wartości dystrybuanty są sporządzone dla u>0. Obliczanie wartości tb(u) dla u<0 umożliwia następująca własność dystrybuanty cl> (rys. 6.5)::

(6.9) 4>(-u) = l-<l»(u) dla każdego u eR.

Prawdziwość tej równości wynika z następujących przesłanek:

I) krzywa y=tp(u) jest symetryczna względem osi rzędnych, 2) zakre-skowane pola na rysunku 6.5 są równe, 3) pole po lewej stronie jest równe <t>(—u), po prawej stronie to l-<P(u).

Rys 6.5.

Tablice kwaniyli u_p ZL U o rozkładzie N(U,1) są sporządzane dla 0,5£p<l. Znalezienie kwantyli u₍, ZL U o rozkładzie N(0,1) dla 0<p<0,5 umożliwia następująca ich własność:

(6-10) ii_p=-u,__p.

Aby uzasadnić tę równość zastosujemy najpierw własność (6.9) dla u = -u_p:

0>(-u_p) = l-<t>(u_p)=l-p. czyli 0>(-u_p)=l-p.

Z ostatniej równości ponownie na podstawie definicji kwantyla danego r/ędu, wnioskujemy że liczba -u_p jest kwantyIcm rzędu l-p ZL U:

-“p=^uH>. czyli u„—u,__p.

♦lu)

Rys 6.6. Rys 6.7.

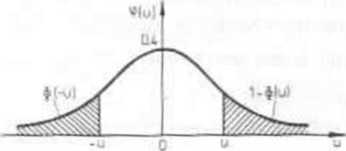
PRZYKŁAD 6.1 ZL U ma rozkład N(0.l). Wyznaczymy a) P(U<1.33), b) liczbę u spełniającą warunek P(U<u) = 0,95.

a) szukane pr-stwo jest wartością dystrybuanty rozkładu N(0,l) dla u = 1,33, (por.rys 6.6):