skan0013

Rozwiązania
1. Obliczając promień zbieżności, mamy:
lim
n—*oo
O-n+1
n~*oo (n + l)4 + 2 n3 +1 n—*oo n3 + 1 :.-|n + l)4 -j- 2
= 1 = 0 =>• = l , .
co oznacza, że szereg jest zbieżny w przedziale (—1,1). Zbadajmy teraz zbieżność tego szeregu na końcach przedziału, czyli w punktach x — -1, oraz x = 1.
Dla x = — 1, mamy szereg naprzemienny postaci
n3 + 1
n4 + 2
’/4=JL
Sprawdzamy, czy są spełnione założenia kryterium Leibniza. Oczywiście mamy
n3 ■
lim bn = lim
►oo n-*oo n4 -j- 2
Można pokazać, że ciąg {6n} jest nierosnący, tzn., że jest spełniona nierówność:
(n +1)3 + 1 n3 +1
~ un
(n + l)4 -f 2 n4 + 2
Na podstawie kryterium Leibniza, szereg Y^(-l)n——- jest zbieżny.
_ . ti 4" 2
n=l
Zbadajmy teraz zbieżność szeregu z zadania 1 dla x = 1, czyli szeregu postaci:
ns + 1
n4 + 2*
Zauważmy, że
n3 +1 na
n4 + 2 2n4 2n
n > 1.
2 n
Ponieważ szereg ^ ~ jest rozbieżny, więc na podstawie powyższej nierówności
i kryterium porównawczego rozbieżny jest również szereg > -
f n4 -ł- 2
nml
Odp.: Przedział [—1,1) jest szukanym przedziałem zbieżności iiiwizmm «>h,u.
2. Obliczmy promień zbieżności:
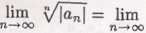
1 r 1 1 1 y— = lim ——— = — \/n2n n—*oo 2 tfn 2
R = 2.
Stąd wynika, że szereg jest zbieżny dla tych x, dla których jest spełniona równość: \x - 2| < 2, czyli dla 0 < x < 4.
Zbadajmy teraz zbieżność szeregu na końcach tego przedziałki^
Dla x = 0, mamy szereg postaci:
Dr1)’
n2n
(_2)» = yv_ 1)lt+1(_ = - f; i,
44? m K § n2n ^ n ’
n=l n=l
a stąd wynika rozbieżność tego szeregu.
Dla x — 4, mamy szereg
n=1 n=l
i wiadomo, że jest on zbieżny.
Odp.: (0,4] jest szukanym przedziałem zbieżności.
Rozwinąć w szereg Maclaurina funkcję
3. f(x) == 3x + sin x cos x
Korzystając z rozwinięcia funkcji sin x, mamy
1 1 -°°^
f(x) = 3x + sin x cosx = 3x + - sin 2x = 3x + - y^(-l)
m
2n+l
2
Wyznaczyć przedziały zbieżności szeregów potęgowych:
Wyszukiwarka
Podobne podstrony:
E 71= 1 (x - 2)" 3n Mamy: 1 I" = 2- Liczymy promień zbieżności szeregu: R = lim
70877 str034 (5) 34 I. ELEMENTY TEORII FUNKCJI ZMIENNEJ ZESPOLONEJ Zadania do rozwiązania 1. Znaleźć
kolo 1. Oblicz granicę ciągów: f b) -1-
2d348486e58b6be6 Kolokwium z matematyki grupa III 1. Obliczyć granicę lim (n + 1) I ■s/n2 + 5 — n) ,
PB032237 Twierdzenie 6.9. Dla każdego a > 0: lim — = o n—-oo fja Wl Twierd
egzamin z majcy EGZAMIN PISEMNY Z MATEMATYKI (1.02.2010) &/v r . (tri3 — 8n li
46 2. Zmienne losowe oraz D2X — lim np( 1 — p) = lim A n—^oo oo2.3.3. Zadania 2.3.
granica ciągu zadania Zadania + Rozwiązania Oblicz granicę: lim (n3 — n + 2) n—> oo » lim (4n‘
226(1) Znaleźć promienie zbieżności szeregów potęgowych o wyrazach zespolonych: 1034 i w 1036. n~0 4
29139 skan0023 (6) 26 Stany skupienia materii Rozwiązanie. 1) Obliczanie ciśnienia a) Według równani
więcej podobnych podstron