Zarz Ryz Finans R1383

1 3. Taksonomia modeli wyceny opcji 383

Jeśli ilości akcji oraz opcji kupna zawartych w portfelu są dobrane w taki sposób, by iloraz QJQ_C równa! się - (dC/dS), pierwsze dwa składniki po prawej stronie równania 13.4 znoszą się, dając zero. Ponieważ zaś są to jedyne człony stochastyczne w tym równaniu, to przekonujemy się, że gdy QS/QC równa się -(dC/dS), zmiana wartości portfela staje się deterministyczna - czyli portfel staje się bezpieczny.

Oznacza to, że przy odpowiednio długiej pozycji w akcjach i krótkiej w opcjach kupna wzrost cen akcji będzie zrównoważony spadkiem wartości krótkiej pozycji w opcjach i na odwrót². Aby zilustrować to zjawisko graficznie, powróćmy do rysunków 13.2 i 13.3. Jeśli ustalimy QJQ_C równe - (dC/dS), nieprzewidywalna zmiana ceny opcji kupna spowodowana zmianą ceny akcji (pokazana na ilustracji 13.2) jest zabezpieczona samą zmianą ceny akcji, toteż pozostaje jedynie przewidywalna zmiana ceny opcji wynikająca ze skrócenia czasu do wygaśnięcia, pokazana na ilustracji 13.3.

Black i Scholes wykazali więc, że gdy liczba akcji i opcji kupna w zabezpieczonym portfelu są stale korygowane odpowiednio do zachodzących w czasie zmian cen waloru, to zysk z portfela staje się pozbawiony ryzyka. Przyjmując w równaniu 13.4 Q_c = - 1 oraz Q_s = (dC/dS), otrzymujemy:

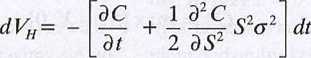
(13.5)

Wyeliminowaliśmy zatem matematycznie wszystkie stochastyczne człony równania (ponieważ czynnik dt jest deterministyczny, również wyrażenie dV_Hjest deterministyczne), nasz zabezpieczony portfel jest wolny od ryzyka. Jego rentowność musi być więc równa stopie zwrotu wolnej od ryzyka:

(13.6)

Możemy teraz wykonać kilka działań, aby wyprowadzić wzór na zmianę ceny opcji kupna. Przyjmując w równaniu 13.1 Q_c = - 1 oraz Q_s - (dC/dS), otrzymujemy:

(13.7)

Następnie podstawiamy równanie 13.7 do równania 13.6:

^: Pełne zabezpieczenie można również osiągnąć dzięki krótkiej pozycji w akcji i diugiej pozycji w opcji kupna. Zauważmy, że wspomniane ograniczenie dotyczy ilorazu QS/QC; nie ma różnicy, w którym z aktywów zajmuje się pozycję krótką.