00098509

306 t. FUNKCJE ZMIENNEJ ZESPOLONEJ

\fiż)dz _Slira^ ACdM

przy czym d. oznacza średnicę podziału przedziału («, jł) na D C

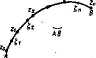
Jeżeli łuk zwykły AB jest zamknięty, a więc jeżeli A - B, to zamiast symbol*; {III. 113) posługujemy się często symbolem

//W* lub \f{z)dz

c c

gdzie C oznacza krzywa Jordana, stanowiącą w tym przypadku łuk AB chcemy podkreślić skierowanie krzywej C, to używamy odpowiednio symbolu

fyj[z)dz albo f(ż)dz

Właśdwwid cdkl (HU 13). Jeżeli funkcje fiz) i h(z) są całkowalne wzdM| hiku AB, zaś K oznacza stałą dowolną, to

j KMd, - K S Md,

' i,^t/w+^wl - s M+ S «<fc

DOWODY tych równości wynikają łatwo z definicji całki (IILl 13). Ponadto mamy

$ /(z)<fc «$ f(z)dz fyf(z)dz~

Uwaga. Całką po toku (krzywej) ciągłym, będącym sumą ewyltłyeh łuków ikkrowaaCftki określa i*ę jako sumą całek po tych hikach.

Istnienie całki (III.U3) jest w ścisłym związku z istnieniem pewnych całek krzywoliniowych par funkcji dwóch zmiennych, o których była mowa w 2-gim tomie tego podręcznika (rozdz. II, p. 5). Oznaczmy mianowicie w(x, y) = Ref(ż), v(x, y) = Im/(z) oraz

Jx_k = ReJz*, Ay_k = ImZlz*, x_k — Ref*. y_k = Imf*

(*= 1,2, ...,»)

a następnie przekształćmy sumę całkową (HI. 112), rozkładając ją na część rzeczywistą i na część urojoną. Otrzymamy

^ Mt)Az_k = ^ y_k)Ax_k-v(x_t, y»>zlyj4-

[»(**, • ODM 17)

Zauważmy, że pierwsza i druga suma po prawej stronie tej równości są to odpowiednio sumy całkowe dla całek krzywoliniowych

$ u(x, y)dx—v(x, y)dy oraz $ o(x, y)</x-j-«(x, y)dy 011.118)

Całka (III. 113) istnieje więc wtedy i tylko wtedy, gdy istnieją obie całki (III.118), przy czym zachodzi wówczas równość

$ /(ż)<fe= ^ udx—vdy+j J vdx+udy (01.119)

AB AB ' AB

którą można przy całkowaniu wykorzystać. Całki <1IL118), a więc i całka (III. 113) istnieją na przykład wtedy, gdy funkcja/(z) jest ciągła na łuku kawałkami gładkim AB. Na ten warunek wystarczający istnienia całki (IILl 13), zaczerpnięty ż nauki o całkach krzywoliniowych skierowanych, będziemy się w dalszym ciągu powoływać.

Obliczanie całki funkcji zmiennej zespolonej poprzez obliczanie całek (III. 118), może okazać się uciążliwe. Wielu rachunków zaoszczędzi nnm następujące twierdzenie. ,

Tir. (o zamianie całki (III.113) na całkę oznaczoną). Jeżeli funkcja flz) jest ciągła na zwykłym luku gładkim AB\ ź — 6(/), t e\(«, /?>, skierowanym zgodnie ze wzrostem parametru, to

Jy(z)& = 5/[z(t)]-z'(t)* (m.i20)

AB w

DOWÓD. Z u»Mł n» przykre Złloimia c*łt* (III-I13) iitcieje. poy czym

J Md*- J ■<*.ridx~v(x,y)dy+j $ ,/)*+«(»•,y)dy

00098509

00098509

\fiż)dz Slira^ ACdM

' i,t/w+*wl* - s M*+ S *«<fc

(*= 1,2, ...,»)

\fiż)dz _Slira^ ACdM

' i,^t/w+^wl - s M+ S «<fc