0344

346
XI. Szeregi nieskończone o wyrazach stałych
a zatem x 1, gdy N -*■ oo. Niech teraz N będzie na tyle duże, żeby: 1) spełniona była nierówność ó*+i < <e2 i 2) odpowiednie x było tak bliskie 1, że zachodzi nierówność
%—O
Wówczas
n-0
co stanowi dowód tezy naszego twierdzenia.
Do rozpatrzonego przypadku szczególnego sprowadza się przypadek ogólny. Wyprowadźmy oznaczenie
v. = a, + 2a2+ ... A-na, (n > 1), »o = 0,
więc
i następnie
00
(7) ^ a„ x'
H«0
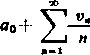
Rot
CD 00
-xf—o0+(i—x) y1 —v*‘ jc*+i .
Z_j n Z—i n (n+1)
Z założeń twierdzenia, tzn. z tego, że vjn -*■ 0, gdy n-+ <x>, łatwo otrzymać wniosek, że
(8) lim (1—0.
*~i-o n
II- t
Dla dowodu rozbijemy tę sumę na dwie
(l-*);£+<l-.x)f]
1 JW+l
i wybierzemy N w ten sposób, aby w drugiej sumie wszystkie współczynniki vjn były mniejsze od z góry danej liczby e >0. Wówczas cała druga suma będzie mniejsza od e dla każdego x. Jeśli chodzi o pierwszą sumę, która ma tylko skończoną liczbę składników, to możemy to samo osiągnąć kosztem przybliżenia x do 1.
Mamy więc wobec (7), (5) i (8)
(n+1)
fl — A—a0 •
Tu możemy już jednak zastosować udowodniony szczególny przypadek naszego twierdzenia, więc także
V—ił—
Z_J n (n+ 1)
n= 1
Z drugiej strony,
n
S
m-1
m (m+1)
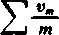
IM— 1

nt—1
Ponieważ pierwszy składnik dąży do zera, wynika stąd, że
lim £ am = A—a0 ,
*-co m-l
co kończy dowód twierdzenia.
Wyszukiwarka
Podobne podstrony:
234 XI. Szeregi nieskończone o wyrazach stałych W przypadku gdy 6 = 1 kryterium to nie pozwala rozpo
256 XI. Szeregi nieskończone o wyrazach stałych Przechodząc do granicy w tej równości dochodzimy na
260 XI. Szeregi nieskończone o wyrazach stałych Stąd ciąg Cauchy’egoe. = ftai ijc
270 XI. Szeregi nieskończone o wyrazach stałych jak wspomnieliśmy jest zbieżny, a zatem jest także
284 XI. Szeregi nieskończone o wyrazach stałych Z drugiej strony, na mocy 391, 4° (gdy przyjmiemy x,
334 XI. Szeregi nieskończone o wyrazach stałych Przejdziemy teraz do dowodu, że Rp(x) dąży do 0, gdy
222 XI. Szeregi nieskończone o wyrazach stałych Jeżeli szereg ma sumę skończoną, to nazywamy go
224 XI. Szeregi nieskończone o wyrazach stałych 364. Podstawowe twierdzenia. Jeśli w szeregu (2) odr
226 XI. Szeregi nieskończone o wyrazach stałych Niech szereg 00 fil+<l2+ •••
228 XI. Szeregi nieskończone o wyrazach stałych Dowód. Wobec tego, że odrzucenie skończonej liczby
230 XI. Szeregi nieskończone o wyrazach stałych Ponieważ jest [77, 5) (a)] lim N-» 99 = 1 , wynika
232 XI. Szeregi nieskończone o wyrazach stałych00 . . (b) 2_j ("ln 2n— 1—* ) TutaJ też posłuż
236 XI. Szeregi nieskończone o wyrazach stałych Nierówność tę można napisać w postaci 1 (n + 1)* J_
238 XI. Szeregi nieskończone o wyrazach stałych Kryterium d’Alemberta nie da się do tego szeregu
240 XI. Szeregi nieskończone o wyrazach stałych to mamy °»tl ^ 1/fn + la. 1/ć. na podstawie twierdze
242 XI. Szeregi nieskończone o wyrazach stałych ność dla x>l. Jeśli zaś x 1, to weźmiemy stosunek
0; 0; 244 XI. Szeregi nieskończone o wyrazach stałych Tym razem 1 a (In ln x)a /« =-!--F(X) at In jr
246 XI. Szeregi nieskończone o wyrazach stałych Sumując je od k = 1 do k = n otrzymamy ogólny wyraz
248 Xi. Szeregi nieskończone o wyrazach stałychi) y—5— (<r>0). iJri/Hn14"/! 1 W tym
więcej podobnych podstron