MATEMATYKA190

370 Vn Macierze. Wyznaczniki, ł/'kłady równań Urnowych
d) Obliczamy rząd mac\crz>' A:
Ponieważ układ ten jest układem jednorodnym, więc R(B) ■ 3 , Zatem R(A)*R(B)*r-3. n- 3 i r*-n . Z twierdzenia Kroneckera - Capcllicgo wynika, źc dany układ ma dokładnie jedno rozwiązanie, a ponieważ jest to układ jednorodny rozwiązaniem tym jest rozwiązanie zerowe: X * y = z «= 0 . ■
PRZYKŁAD 2.4 Rozwiążemy układ równań:
1,
0,
-1.
2;
2x + y-2z-u = I.
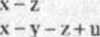
0)
— i.
x + 2y-z-2u = 2;
Jest to układ 4 równań o 4 niew iadomych Ponieważ
2 1-2-1 1 0 -I 0 n I -1 -1 1 =0 1 2-12
więc obliczyć należy' rzędy macierzy A i B Łatwo otrzymujemy, że R(A) = R(B)= r = 2 .
Z twierdzenia Kroneckera - Capcllicgo wynika, że układ ten ma nieskończenie wiele rozwiązań i są one zależne od dwóch parametrów.
Spośród równań układu (ł) wybieramy dwa równania - np drugie i trzecie - z niewiadomymi x i y, a pozostałe niewiadome traktujemy jako parametry: z » zq. u = u0. Otrzymujemy w ten sposób układ pomocniczy
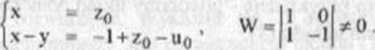
(2)
Układ ten ma jedno rozwiązanie: x*ZQ,y *1 + u0. Zatem rozwiązaniem układu (1) jest każda czwórka liczb: x = /<>. y = 1 + u0, z » zq , u = u0, gdzie z0, u0 są dowolny mi liczbami rzeczywistymi.
PRZYKŁAD 2.5 Zbadamy liczby rozwiązań następującego układu równań w zależności od parametru a .
ax-2y + z ■ -3, x-ay + 2z » 1.
2x-ay + /. ■ 2.
Obliczamy wyznacznik główny tego układu:
W
a2 +u-6
a -2 1 ł -a 2 2 -a 1
Jeżeli W =a2 +a-6*0, czyli a*2 i u*-3, to układ ma, zgodnie z twierdzeniem Cramera, dokładnie jedno rozw iązanie.
Dla a = 2 otrzymujemy układ postaci
|
2x-2y + z - |
-3, |
|
x - 2y + 2z = |
1, |
|
2x-2y + z = |
2. |
który nic ma rozwiązania - jest sprzeczny (wystarczy porównać pierwsze i trzecie równanie) Dla a = -3 mamy
' f-3x-2v + z = -3.
\ x + 3 y + 2/. = L I 2x + 3y + z = 2.
Łatwo obliczyć, że dla tego układu R(A) = R(B) = 2. Zatem układ ma nieskończenie wiele rozwiązań i są one zależne od jednego parametru
Podsumujmy: rozważany układ równań ma jedno rozwiązanie, gdy a * 2 i a *■ -3; jest sprzeczny, gdy a - 2 oraz ma nieskończenie wiele rozwiązań, gdy a = -3. ■
ZADANIA DO ROZWIĄZANIA.
I. Rozwiązać układ równań:
(3x — 2y = 0. a) |x-y + 2z = 1.
(y + /. ■ -t
3x + y + u » 0, y - z - u “ 0, 2x+z+u * 0, 2y - z- 2u = I;
b)
x - y - z X I 2/. 4 II x + y + u 2v-z- u
c)
x-y-z x + 2z - u x + y + u 2y - z - u
= -3.
* -I. = -3. - 0;
* 0. o.
» 0,
* 0;
Wyszukiwarka
Podobne podstrony:
MATEMATYKA190 370 Vn Macierze. Wyznaczniki, ł/ kłady równań Urnowych d) Obliczamy rząd maccrz> A
MATEMATYKA190 370 Vn Macierze. Wyznaczniki, ł/ kłady równań Urnowych d) Obliczamy rząd maccrz> A
MATEMATYKA184 358 vn Macierze. Wyznaczniki. Układy równań liniowych ZADANIA DO ROZWIĄZANIA 0 0 0 0 0
22064 MATEMATYKA189 368 Vn. Macierze. Wyznaczniki. Układy równań liniowych 368 Vn. Macierze. Wyznacz
47137 MATEMATYKA188 366 vn Macierze. Wyznaczniki. Układy równań liniowych (24) allxl a2lxl + a„x2 +
MATEMATYKA179 348 VII Macierze Wyznaczniki Układy równań liniowych --— x aII. ai2 at3, a2ly. a22,
MATEMATYKA183 356 VII. Macierze. Wyznaczniki. Układy równań liniowych kolumny tworzymy minory drugie
20944 MATEMATYKA186 362 VII. Macierze. Wyznaczniki. Układy równań liniowychw, w2 wn _ a,,x,+a,2x2+ .
MATEMATYKA191 372 VH Macierze. Wyznaczniki. Układy równań liniowych 2. e) 2x2 -6x3 + 2x4 2x,-x2+x3&n
więcej podobnych podstron