Untitled Scanned 16

32 -

niu tzw. operacji akieJania - łączeń par iloczynów lub sum, różniących się Jednym tylko znakiem negacji. Wykorzystuje rię przy tym przekształcenia

a-b + a-b = a* (b + b) = a* 1 = a (a + b)»fe + b) = a + b*b = a

Oto kolejne etapy przekształcania kanonicznej postaci alternatywnej funkcji, zdefiniowanej w tabl.2.4

y — V ■ V a V J. W . *r « W X W • T • T X *r a T • TT X

W drugim etapie sklejania środkowy składnik wykorzystano dwukrotnie. Jest to możliwe, bo a =* a + a +... Ten sam wynik uzyskać można drogą sklejania czynników kanonicznej postaci koniunkcyjncj

y o + x₂ + + x₂ + = x₁ + x₂

W wyniku sklejania otrzymuje się wyrażenia, które zachowują postać sumy iloczynów albo iloczynu sum, lecz nie są już postaciami kanonicznymi. Wyrażenie tego typu nazywane są postaciami normalnymi: normalną postacią alternatywną albo normalną postacią koniunkcyjną.

Ponieważ zwykle operacje sklejania w danej postaci kanonicznej przeprowadzać można kilkoma sposobami, nie zawsze końcowy wynik sklejeń ma postać najprostszą spośród możliwych. Na przykład, sklejając w innej niż poprzednio kolejności ekładni-ki postaci kanonicznej tej samej funkcji, otrzymuje się bardziej złożoną postać normalną

+ + x.j'X2*x.

x^«x₂«x^ + x.j'X₂*X2 + x_<j»x₂^,X2 +

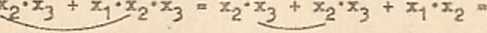
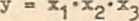
⁺ *T^:

= X₂ + X.j • Xg

w której nie ma już możliwości sklejania (uzyskane wyrażenie można, wykorzystując prawa algebry Boole*a, przekształcić do poprzednio otrzymanej postaci: z₂ + ⁼ ^2 ⁺ *1 ^ * ^^x2^{+ x}2^ ⁼

= Cx₂ + x₁ ) • 1 x₂ + x₁ ).

Postać normalna alternatywna (koniunkcyjna) funkcji logicznej zawierająca najmniejszą liczbę symboli operacji logicznych spośród wszystkich innych alternatywnych (koniunkcyjnych) postaci normalnych tej samej funkcji nazywa się minimalną alternatywą (koniunkcyjną) postacią normalną.

Niekiedy możliwa jest dalsza minimalizacja minimalnej postaci normalnej danej funkcji, polegająca na wyciąganiu przed nawias wspólnego czynnika albo składnika. Operacja ta nazywa się faktoryzacją.

Iloczyny, występujące w normalnej postaci alternatywnej, w której nie ma już możliwości sklejania są tzw. implikantami prostymij analogicznie sumy w normalnej postaci koniunkcyjnej - implicentami prostymi.

Impiikantem funkcji f Jest funkcja g tych samych argumentów gdy dla wszystkich stanów argumentów, dla których g«1 także f=1. Impiikantem prostym nazywany jest elementarny iloczyn, który jest impiikantem i który zmniejszony o dowolną literę przestaje być impiikantem.

Implicentem funkcji f jest funkcja h tych samych argumentów gdy dla wszystkich stanów argumentów, dla których h=»0 także f*=0. Implicentem prostym nazywana jest elementarna suma, która jest implicentem i która zmniejszona o dowolną literę przestaje być implicentem.

Poszukiwanie minimalnych postaci normalnych sprowadza się do wyboru najkorzystniejszego zestawu prostych implikantów albo prostych implicentów. Opracowano szereg metod usprawniających ten proces. Do najbardziej znanych należą metoda Karnaug-ha i metoda Quine'a-McCluskeya,

2.3.1. Metoda Kamaugha

Istota metody polega na specjalnej formie tablic wartości funkcji, zwanych tablicami Karnaugha - rys.2.1. Pola wewnątrz