17567 Obraz (12)

202 Dziecko jako naukowiec: Piagetowska teoria rozwoju poznawczego
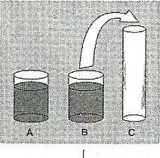
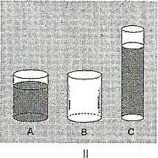
Eksperyment badający zasadę zachowania objętości

Dlaczego ten prosty eksperyment był tak ważny? Była to w istocie jedna z sze- • regu demonstracji ilustrujących, że zasada zachowania stałości dotyczy wielu cech przedmiotu, między innymi długości, liczby, masy, wagi i powierzchni, jak również objętości (szczegóły zob. ramka 6.3). Wszystkie wykazały, że myślenie dzieci na temat świata przechodzi (jak mawiał Piaget) od poziomu percepcji do pozio- . mu logiki. Wróćmy do powyższego przykładu. Kiedy nalejemy wodę do naczynia C, ocena przedszkolaka będzie zdominowana przez jedną z cech wyglądu tego W naczynia, mianowicie jego wysokość. Po przelaniu z naczynia B, poziom wody podniesie się, a wniosek z tego jest taki, że teraz jest jej więcej. Małe dzieci nie potrafią uwzględniać jednocześnie dwóch cech - wysokości i szerokości. Nie są więc jeszcze zdolne zrozumieć, że zmiana jednej wielkości kompensuje zmianę7-drugiej. Podobnie, przedszkolak nie potrafi wyobrazić sobie odwrócenia sytuacji i zrozumieć, że przelanie wody z powrotem z naczynia C do B sprawi, że poziom i wody powróci do stanu poprzedniego. To wymaga myślenia operacyjnego, które pojawi się dopiero po okresie przedszkolnym i umożliwi logiczne rozwiązywanie problemów, a nie opieranie się na znamiennych, ale jednak nieistotnych wrażeniach percepcyjnych.
Badanie dziecięcego rozumienia zasady zachowania stałości
Piaget opracował szereg zadań mających na celu zademonstrowanie istoty myślenia dziecka, a do najbardziej znanych należą eksperymenty badające zasadę zachowania stałości. W każdym przypadku zamierzał wykazać, iż pojęcie przedmiotu u dzieci w wieku przedszkolnym zdominowane jest przez widoczne właściwości percepcyjne, i że dzieci te łatwo zwieść poprzez pozorne zmiany wyglądu. Natomiast dzieci starsze, w stadium operacji konkretnych, zdają sobie sprawę z tego, że zmiany te są nieistotne dla zasadniczych cech przedmiotu, i dlatego rozumieją zasadę zachowania jego podstawowych właściwości.
Zastanówmy się nad zasadą zachowania stałości liczby (zob. ryc. 6.3). Dziecko widzi dwa równo ułożone rzędy guzików; widzi, że jest ich taka sama liczba w każdym rzędzie. Następnie guziki z jednego rzędu zostają na oczach dziecka rozsunięte. Pada pytanie o to, czy liczba guzików w obu rzędach jest nadal jednakowa. Przedszkolaki odpowiedzą, że teraz w dłuższym rzędzie jest ich więcej. A jeśli zsuniemy je do siebie tak, że rządek stanie się krótszy, powiedzą, że jest ich mniej.
mmmmm_mmmmm
mmmmm mmmmm
Zachowanie stałości liczby
Zachowanie stałości masy
RYCINA 6.3_
Zadanie na zachowanie stałości liczby, długości i masy
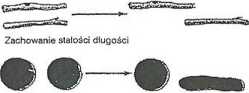
By zbadać zasadę zachowania stałości długości, układa się równolegle dwa patyczki jeden nad drugim. Dziecko potwierdza, że są równe. Następnie jeden patyczek zostaje wysunięty tak, że wystaje poza drugi. Pada pytanie, czy są tej samej długości. Przedszkolak zostanie zwiedziony tym przesunięciem i stwierdzi, że patyk wysunięty jest teraz dłuższy.
Następny przykład dotyczy zachowania stałości masy. Przed dzieckiem leżą dwie równe kulki plasteliny. Dziecko potwierdza, że zawierają jednakową ilość plasteliny. Jedna z nich zostaje następnie uformowana w wałeczek. Na pytanie, czy obydwie kulki zawierają taką samą ilość plasteliny, przedszkolak odpowie, że w wałku jest jej teraz więcej.
Na pytanie o powód swych odpowiedzi, dzieci w stadium przedoperacyjnym bez wahania wskazują na to, co widzą. Dlatego wskazując wałeczek plasteliny powiedzą: „Jest dłuższy” albo „Zrobiłeś tak, że patyk sięga dalej”. Natomiast wyjaśnienia dzieci w stadium operacji konkretnych wskazują, że dokonane zmiany są dla nich bez znaczenia, np.: „Nie odejmowałeś plasteliny, więc musi być tyle samo.”, „Wałek jest dłuższy, ale cieńszy." lub „Możesz znowu zrobić kulkę i nadal będzie tyle samo.”.
Te trzy ostatnie objaśnienia pokazują, ilu rozmaitych operacji wymaga zrozumienie zasady zachowania stałości. Pierwsza skupia się na zasadniczej tożsamości przedmiotu - kiedy to nic nie zostało dodane ani odjęte. Druga odnosi się do kompensacji, tzn. zmiana jednej wielkości jest kompensowana przez zmianę drugiej. A trzecia wskazuje na odwracalność myślenia starszych dzieci. Potrafią one wyobrazić sobie, co się5stanie, gdy wałeczek z powrotem zmienimy w kulkę, i na tej podstawie dochodzą do wniosku, że zmiana kształtu nie ma wpływu na ilość plasteliny.
Wyszukiwarka
Podobne podstrony:
22114 Obraz (10) 198 Dziecko jako naukowiec: Piagetowska teoria rozwoju poznawczego Stadia rozwoju
Obraz (14) 206 Dziecko jako naukowiec: Piagetowska teoria rozwoju poznawczego i w ten sposób poszerz
Obraz (16) 210 Dziecko jako naukowiec: Piagetowska teoria rozwoju poznawczego dla rozwoju poznawczeg
38933 Obraz (18) 214 Dziecko jako naukowiec: Piagetowska teoria rozwoju poznawczego Literatura uzupe
23945 Obraz (13) 204 Dziecko jako naukowiec: Piagetowska teoria rozwoju poznawczego Podkreślmy raz j
więcej podobnych podstron