26916 P1111263
32 VIII. Funkcja pierwotna (całka nieoznaczona)
ków A, M, N. Ponieważ liczniki grupy ułamków (5) zawierają k współczynników, a liczniki grupy ułamków (6) 2m współczynników, przeto na mocy (4) jest ich razem n. Dla wyznaczenia wspomnianych współczynników stosuje się zwykle metodę współczynników nieoznaczonych. Polega ona na tym, że znając kształt rozkładu ułamka P/Q, piszemy go po prawej stronie ze współczynnikami nieoznaczonymi w licznikach. Współ-nym mianownikiem wszystkich ułamków prostych jest oczywiście Q, dodając je otrzymujemy ułamek właściwy (*). Jeśli odrzucimy teraz z lewej i z prawej strony równości mianownik Qy to otrzymamy równość dwóch wielomianów stopnia (/j—1) będącą tożsamością względem x. Współczynnikami przy różnych potęgach wielomianu po prawej stronie będą jednorodne wielomiany liniowe względem n nieoznaczonych współczynników. Przyrównując je do odpowiednich współczynników liczbowych wielomianu P, otrzymujemy wreszcie układ n równań liniowych, z których wyznaczymy współczynniki literowe. Ponieważ możliwość rozkładu na ułamki proste została udowodniona, wspomniany układ nigdy nie może być sprzeczny.
Co więcej, wspomniany układ równań liniowych ma rozwiązanie jakikolwiek będzie zespól wyrazów wolnych współczynników wielomianu P, a zatem wyznacznik tego układu musi być różny od zera. Innymi słowy, układ ten jest zawsze oznaczony. Ta prosta uwaga dowodzi jednocześnie jednoznaczności rozkładu ułamka właściwego na ułamki proste. Objaśnimy to, o czym mówiliśmy, na przykładzie.
2x2-f 2x+13 (x—2) (x2-H)2 '
Przykład. Niech będzie dany ułamek rozkład
Na mocy ogólnego twierdzenia ma on
2x2+2x+13 A ■ Bx+C . Dx+E
(x-2)(x2+l)2 x—2 x2-fl (x2+l)a |
Współczynniki A, B, C, D, E wyznaczymy z tożsamości
2x2+2x+13-4 (x2+l)2-M£x-rC)(x2 + l) (x-2)+(Dx+£)(x-2) .
Przyrównując współczynniki przy jednakowych potęgach x po lewej i po prawej stronie równości otrzy* snujemy układ pięciu równań
x* 4+/?- 0, x2 -2£+C«0, x2 2A+B-2C+D = 2, x* -20+C-2D+E-2, x° 4—2C—2£ — 13 .
Stąd
4-1, £«-!, C — —2, D --3, £- -4.
Ostatecznie
2x2-f 2xt-13___1 x+2___3x+4
U-2)(xi+Di ~ x—2 x2+l (x2+l)a I
Stwierdzony powyżej fakt algebraiczny ma bezpośrednie zastosowanie do całkowania funkcji wymiernych. Jak widzieliśmy w ustępie 273, ułamki proste można scałkować w postaci skończonej. Możemy to samo powiedzieć teraz o dowolnym ułamku wymiernym.
(ł) Suma ułamków wymiernych właściwych jest znowu ułamkiem właściwym.
Jeśli przyjrzeć się tym funkcjom, za pomocą których wyrażają się całki wielomianów i ułamków właściwych, to można sformułować wynik ten dokładniej:
Całka dowolnej funkcji wymiernej wyraża się w postaci skończonej przez funkcję wymierną, logarytm i arcus tangens.
Wracając do rozpatrzonego powyżej przykładu i przypominając sobie wzory z ustępu 273 otrzymujemy
2x*+2x+13
(x-2) (xa+l)2
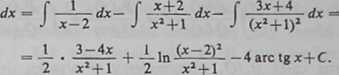
/
276. Wydzielenie części wymiernej całki. Istnieje sposób podany przez M. W. Ostro -gradskiego, za pomocą którego obliczanie całki wymiernego ułamka właściwego znacznie się upraszcza. Sposób ten pozwala drogą czysto algebraiczną wydzielić część wymierną całki.
Widzieliśmy [273], że składniki wymierne całki otrzymujemy przy całkowaniu ułamków prostych postaci II i IV. W pierwszym przypadku całkę można napisać od razu.
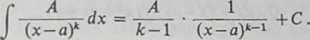
Zbadajmy teraz, jaką postać ma część wymierna całki
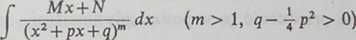
Stosując znane nam już podstawienie x+yP = t wykorzystujemy równości (1), (2) i wzór
redukcyjny (6) z ustępu 271 dla n = m—\. Gdy wrócimy do zmiennej x, otrzymamy
/ (*
Mx+N I M'x+N'
> . — . _xni- dx =
:2+px+q)m (x2 +px+q)m~l
dx
(x2+px+q)m~i *
gdzie M', N' i a oznaczają pewne współczynniki stałe. Na mocy tego samego wzoru zastępując m przez m— 1, otrzymujemy dla ostatniej całki (jeśli m > 2)
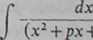
r_« ax__ M x+N - _*
J (x2+px+qyn~l (x2+px+q)m~2 §| -q)"~z
itd., dopóki nie sprowadzimy wykładnika potęgi trójmianu x2 +px+q w całce po prawej stronie do jedności. Wszystkie wydzielane kolejno wyrazy są ułamkami właściwymi. Łącząc je razem otrzymamy wynik w postaci następującej:
f Mx+N . _ R (x) , r dx _
* \ J (x2+«px+fl)M (x2+px+q)m~l J x2+px+q *
gdzie R (x) jest wielomianem stopnia niższego niż mianownik (*), a A jest stałą.
(l) Patrz odsyłacz na str. 32.
3 Rachunek różniczkowy
Wyszukiwarka
Podobne podstrony:
32 V1U. Funkcja pierwotna (całka nieoznaczona) ków A, M, N. Ponieważ liczniki grupy ułamków (S) zawi
21923 P1111252 10 VIII. Funkcja pierwotna (całka nieoznaczona) Jeśli konkretnie dana funkcja ma punk
71760 P1111253 12 VIII. Funkcja pierwotna (całka nieoznaczona) III. Jeśli to J f(ax+b) dx *= — F (ax
P1111275 56 VIII. Funkcja pierwotna (całka nieoznaczona) Dla obliczenia całki 56 VIII. Funkcja pierw
19763 P1111255 16 VIII. Funkcja pierwotna (całka nieoznaczona) Przypuśćmy, że trzeba obliczyć całkę
P1111253 12 VIII. Funkcja pierwotna (całka nieoznaczona) III. Jeśli to J f(ax+b) dx *= — F (ax+6)+C
więcej podobnych podstron