DSC07362

142

Geometria analityczna w przestrzeni

dla pewnego UR\{0}. Mamy fi = (1,1,1) oraz SP= (-z, 1 - y,3 - z). Współrzędne punktu 5 spełniają układ równań

x + y + * = 0,

—z _ 1 — y _ 3 — z ¹ ~ ¹ '

Układ ten jest równoważny układowi

z + y+i = 0,

-x + y =1.

m + $=3.

r<-* 5

^Z~T

Rozwiązaniem tego układu jest trójka liczb z = y = —i,

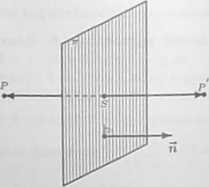
II sposób wyznaczania S. Zauważmy, że prosta ( : z = t,y — 1 + t,z — 3 + t, gdzie t 6 R, przechodzi przez punkt P i jest prostopadła do płaszczyzny ir. Punkt S = (t, 1 +1,3 + t) jest punktem przecięcia prostej l i płaszczyzny ir. Jego współrzędne wyznaczamy z zależności t + (1 +

t) t (3 + t) = 0. Stąd t = ——, zatem ⁵= (^-|’ ^-|’ |) ■ Znajdziemy teraz punkt P‘. Niech P‘ = ^z',j/',z'^. Wtedy

i -1

oraz

(f.MV

Współrzędne punktu P' znajdziemy z układu równań

liii

,•-!«.i

3 3*

— Zatem P

Rozwiązaniem tego układu jest trójka liczb z” = 5

(8 _5 I ³ ~3’^:

V 3’- 3'3j‘

• Przykład 5.21

Znaleźć rzut ukośny w kierunku wektora 3 = (1, —1,1);

a) punktu P = (0,1,0) na płaszczyznę it: x + 3y — 0 = 0;

b) prostej l: x = —2y = 3z na płaszczyznę zr: x + y +z — 5 >

Przykłady

143

a) Rzut punktu P na płaszczyznę n w kierunku wektora tZ» jest punktem przecięcia prostej l o wektorze kierunkowym w. poprowadzonej przez punkt P, z płaszczyznę ir (rysunek). Znajdziemy najpierw równanie prostej l o wektorze kierunkowym ta = (1,—1.1) prze-chodza_cej przez punkt P = (0,1,0). Mamy

Wyznaczymy teraz punkt P = (x, y, z) przecięcia prostej l z płaszczyzną ir. Współrzędne tego punktu spełniają układ równań

\^B

x _y-l z

1 -1 T’

z + Zy — 6 = 0.

Rozwiązaniem

^{1 =} ~2* » I

V 2’ 2’ 2)'

tego układu jest trójka liczb

5 3 „ ■EW

2- - = - j- Zatem P =

b) Rzut prostej l na płaszczyznę n w kierunku wektora ui wyznaczymy w następujący sposób. Na prostej l wybieramy dwa dowolne punkty A i B. Następnie znajdu-jemu ich rzuty A i B' na płaszczyznę -w kierunku wektora tu. Rzutem prostej l na płaszczyznę jt w kierunku wektora w będzie wtedy prosta / przechodząca przez punkty A i B (rysunek). DJa uproszczenia obliczeń wygodnie jest przyjąć, że A jest punktem przecięcia prostej i z płaszczyzną TT. Wtedy oczywiście A = A. Niech A = (x,p, z). Współrzędne punktu A spełniają układ równań

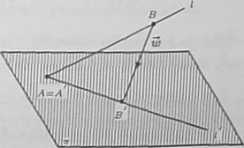
x = —iy — 3z, x + y + z — 5 = 0.

Rozwiązaniem tego układu jest trójka liczb x = 0, y = —3, z = 2. Zatem A = (6, —3,2) = >T. Wybieramy teraz dowolny punkt B = fx\y',z’^ £ A na prostej /. Przyjmują?

np. x = 0 otrzymamy p = 0 oraz z = 0. Postępując podobnie jak w punkcie a) tego przykładu znajdziemy rzut ® = (5, —5,5) punktu i? na płaszczyznę jt w kierunku wektora ui. Teraz znajdziemy równanie prostej ł' przechodzącej przez punkty A' i B'. Mamy

j f* = : ,6— t,.-W

ł : < p = — 3 — 2t, gdzie t 6 R.

(. - = 2 + 31,