Image0012 BMP
.2.4. Operator nabla
Podstawowe o|X'racjc różniczkowe analizy wektorowej, a mianowicie gradient, dy-crgcncję i rotacja, można przedstawić w sposób formalny za pomocą operatora wekto-twego zwanego operatorem nabla, bądź, krótko nablą, bądź też operatorem Hamiltona. iperator nabla jest formalnym wektorem i określony jest. wzorem
V=va--+i,^-+vf-; o-30)
ax ov oz
:st to zatem suma geometryczna trzech operatorów różniczkowania. Mnożąc nablę przez skalar <p, otrzymujemy
o r
dę
-h lt ; = grad <p,
oz
(1.31)
więc gradient skalara. Tworząc iloczyn skalamy nabli przez wektor A, znajdujemy godnie z określeniem iloczynu skalarnego
3AX vA V-A= ■+■■■-0x 3y
DA.
y '■ ‘ = div A.
3 z
(1.32)
ryli dywergencję wektora. Natomiast iloczyn wektorowy nabli i wektora A przybiera jstać
V
xA=
(3A2
\ 8y

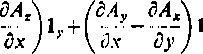
ot A,
tyli równa się rotacji wektora.
Tożsamości wektorowe (1.29) przy zastosowaniu nabli przybierają postać:
VxVp = 0, V-(VxA) = 01 (1.33)
laplasjan
*2 ^2 -2
, 3 3 o
va=vv=;-
coc* 3y~ cs
st sumą trzech operatorów różniczkowania drugiego rzędu.
Laplasjan wektora w układzie współrzędnych prostokątnych określimy za pomocą zoru
0-34)
(1.35)
yli
V2A = V2(M,-tA,At+1sA=), v2a=ix v2ax+1 ‘ V2Ay+1, VZAZ.
iplasjan wektora w układzie współrzędnych prostokątnych jest więc sumą geometryczną plasjanów składowych tego wektora. Tak proste wyrażenie dla laplasjan u wektora jest awdziwę tylko w prostokątnym układzie współrzędnych, a w innych układach otrzy-uje się złożone wzory.
Operator nabla jot określony w układzie współrzędnych prostokątnych, jednakże ruttaty olizj manę przy zastosowaniu tego operatora są prawdziwe w dowolnym ukła-ie współrzędnych.
Operator na lila można stosować przy obliczaniu złożonych operacji wektorowych, u sanie ohlie/cnia sprowadzają się do prostych działań algebry wektorowej. Tak na przykład otrzymuje się
V-(AxB) = B-VxA —A-VxB,\
(1-36)
V x (ęk)~ęSt x A + Vę» x A, 1
V x(V x A) = V(V 'A) —V2A, J
czyli
(137)
div(Ax B) = B-roi A —A • roi B, 1 rot(pA)= protA+grad ętx A,| rot rot A = grad di v A — V2A. J
1.2.5. Twierdzenie Gaussa-Ostrogradskiego. Twierdzenie Stokesa
Twierdzenie Gaiis.sa-Osirogradskiegu zwane również twierdzeniem Gaussa głosi, że strumień wektora przez powierzchnię zamkniętą jest równy całce objętościowej dywergencji tego wektora w obszarze, którego granicą jest wspomniana powierzchnia, cz.yli
j A-dS= | div Ada. (1.38)
Sit) •’
Twierdzenie to można interpretować jako przekształcenie całki powierzchniowej na całkę objętościową.
Pole wektorowe jest polem bezźródiowym lub solenoidalnym w obszarze, gdy dywergencja wektora pola jest równa zeru w każdym punkcie tego obszaru. Na podstawie twierdzenia Gaussa-Ostrogradskiego wnioskujemy, że w polu bezźródiowym strumień wektora pola przez dowolną powierzchnię zamkniętą równa się zeru. Wynik ten można interpretować w ten sposób, że strumień wypływający z pewnego obszaru przez jego granicę równa się strumieniowi wpływającemu do wnętrza tego obszaru.
Pole wektorowe jest źródłowe w obszarze, gdy dywergencja wektora jest różna od zera w tym obszarze lub w jego części. Zgodnie z twierdzeniem Gaussa-Ostrogradskiego wnioskujemy, że strumień wektora poła przez powierzchnię zamkniętą ograniczającą obszar, w którym pole jest źródłowe, nic zanika i jest wielkością różną od zera.
Twierdzenie Stokesa głosi, że całka liniowa wektora pola wzdłuż krzywej zamkniętej równa się strumieniowi rotacji tego wektora przez powierzchnię, której brzegiem jest wspomniana krzyw-a, czyli
Adl = j rot A* dS. ' (1-39)
Clffl
Twierdzenie Stokesa można interpretować jako przekształcenie całki liniowej na całkę powierzchniową.
Pole wektorowe jest polem be żwirowym w obszarze, gdy rotacja wektora jest rnwnu zeru v. każdym punkcie tego obszaru. Zgodnie z twierdzeniem Stokesa, w polu he/.wiro-wym całka liniowa wektora pola wzdłuż, dowolnej krzywej zamkniętej równa się zeru.
Pole wektorowe jest polem iririwiw, gdy rotacja wektora pola jest rożna od zeru w tym obszarze lub w jego części.
Wyszukiwarka
Podobne podstrony:
Podstawowe wzory algebry i analizy wektorowej Podstawowe wzory algebry i analizy wektorowej Tożsamoś
86271 Ziemniak (3) Podstawowe wzory algebry i analizy wektorowej Tożsamości algebraiczne: A+B=B+A, A
Image0089 BMP gdzie: L jest krzywą brzegowy powierzchni S. Ponieważ wektor dl jest prostopadły do 1a
1tom152 6. ELEKTROTECHNIKA TEORETYCZNA 306 Tablica 6.10. Elementy analizy wektorowej, wg [6.6]Operat
49219 Image00016 charakterystyki częstotliwościowe elementów podstawowych Lp Transmiuncja operator
Image0013 BMP 1.3. Wielkości charakteryzujące pole elektromagnetyczne .3.1. Określenia i zależności
Image0018 BMP 1.7. Prawo zachowania ładunku Na podstawie I prawa Maxwella „ T SD rot H=J +
Image002 bmp KROK III *PROCES RÓWNOWAGI PROCES POBUDZANIA PROCES HAMOWANIA PODSTAWIAMY WIELKOŚCI PO
Image0023 BMP po podstawieniu K«* -grad V. mamy divgrad V P e żyli (2.30) ;dzie V2 jest lapJasjanem
Image0025 BMP wobec czego nu podstawie drugiego wzoru (2.51) otrzymujemy A2a,+ ;=o, a stąd A 2 — ~ A
Image0031 BMP I mtlinkj i, ora/ i. (luj;) ię ł:il w o obliczyć na podstawie tikl.ulu / ryv &nb
Image0072 BMP i podobnie dH Ot d 8t (7.37) Po podstawieniu wzorów (7.35)-(7.37) do równania (7.33),
Image0074 BMP gd/ic: T o/.iuic/u okres omawianych wielkości. Podstawiając składowe wektora Wf z wyra
Image0078 BMP wobec czego wobec czego (8.55) c P+)Q = I*Ę*dl. zgodnie ze wzorem (8.54). Po podstawie
Image0104 BMP rswę/enlr polu magnetycznego obliczamy ze w/oni i pu podstawieniu zależności (10.33) i
Image0107 BMP 1.2. Metoda rozdzielenia zmiennych .2.1. Określenia i zależności podstawowe Przedmiote
Image0108 BMP I’r/y analizie pul elektromagnetycznych c/.yslo spotyka uę zagadnienie brzegowe dla óu
więcej podobnych podstron