36 VIII. Funkcja pierwotna (całka nieoznaczona)

Tak więc szukana całka jest równa

4jc¹4-4x^s+16x¹ + 12x+8

/

(jr+D^+J)²

dx = i

x²-x+4

.^-ł-j^+Ar+l    ' " J ¹² +

x²—x+4

-+3 f —f^x 2.

1 J x²+l +3 arc tg x+C.

x³+x²+x+l

W przykładzie tym obliczenie ostatniej całki można było łatwo wykonać od razu. W innych przy. padkach trzeba znowu rozkładać na ułamki proste. Można zresztą czynność tę połączyć z poprzednią;

277. Przykłady. Podamy dalsze przykłady całkowania funkcji wymiernych.

1) f    Rozkład na ułamki proste otrzymujemy tu poprzez nieskomplikowane prze-

J x²(l |pp)J kształcenia

1    _ (l+x²)-x² j 1___1_| (l+¹²)-x²    _    1    ₌

x²(l+x²)²    “ jc^I+jc²)² "    jc²(1+x²)    (1+¹²)^2    12(l+x²)    (ł+x²)²

1

1

1 -f x² (1 +x²)²

Odpowiedź: -J-J- _1+x

^X T~\^1XCtgJC+c1

iii®

4x²+4x-U

(2x-l)(2x+3)(2x-5)

• dx.

Mamy

4x²+4x-11

±_x2+±_x--± 2^2 8

— +

-z- +

(2¹-l)(2¹+3)(2¹-5)    (j:— y)(¹+ j)(^1_ y)    \    ¹+y ¹-f ’

skąd wynika tożsamość

łf+iS-l (¹+ BI ^+b(^x- HI +^c (¹- iM¹+11

Zamiast przyrównywać współczynniki przy jednakowych potęgach ¹ w obu stronach równości, moż-! na postąpić inaczej. Podstawmy w tej tożsamości kolejno x =    ~~. Otrzymujemy od razu i

A r= -L _t b =¹ ——, C «=    , przy każdym bowiem podstawieniu z prawej strony pozostaje tylko jedeni

składnik.

Odpowiedź: -^In Jx— -^-j —|¹:t^ 2'j"¹' "s    \j la^ p g"

3) I ^

+ CV)i

**+¹    x²+x/2+l    x²-x]/2+l

1 ~{Ax+B)(x²-xfó+\)+i.Cx+D)(x²+x}/2+\)

x*

skąd

otrzymujemy układ równań

Tak więc

**

x°

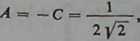
B = D -

2 '

/

dx

x*+l

i r x+vT

2}/2 ^ x*+a:}/2+1

1_ _ln x²-ł-xj/2+l 41/2 J^-AryT+l

dx— •

■J

t—yT

2|/2 ^J x*-xyT+i

-dx <

+

2 >/2*

arctg (*yT+i)+

2|/2

arctg(x|/2-l)+C.

tak więc

X⁴

x^s

x^a

X¹

x°

skąd