094 2

186 X. Badanie przebiegu zmienności funkcji

10.3. Funkcja /(x) = |x|-2 ma dwa miejsca zerowe: x=-2 i x = 2. Czy można za stosować twierdzenie Rolle'a do tej funkcji w przedziale -2s%xs$2? Sporządzić wy]^ i wyjaśnić.

10.4. Zastosować twierdzenie o wartości średniej do funkcji f(x) = _sJx, przyjmy a= 1, b = 9 i znaleźć wartość x = c, o której mowa w twierdzeniu. Sporządzić szkic.

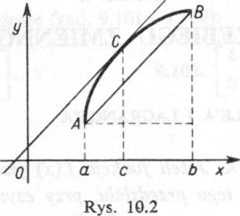
10.5. Czy można zastosować twierdzenie Lagrange’a, do funkcji f(x) = l/x w przedziale — 1 <x<4? Podać interpretację geometryczną.

10.6. Zastosować twierdzenie Lagrange'a do funkcji / (x) = x² w przedziale a^x^b i znaleźć wartość x = c, o której mowa w twierdzeniu.

10.7. Twierdzenie Lagrange’a może być napisane w postaci

f(x + h)—f(x) = hf'(x+6h), gdzie 0<0<1.

Zastosować tę postać do funkcji a) f(x) = x², b) f(x) = x³ i wykazać, że w przypadku: a) 0 nie zależy ani od wartości x, ani od wartości h, b) 0 zależy zarówno od x, jak i od h.

§ 10.2. BADANIE PRZEBIEGU ZMIENNOŚCI FUNKCJI. EKSTREMA FUNKCJI

Badanie przebiegu zmienności funkcji opiera się na następujących twierdzeniach podstawowych (będących wnioskami z twierdzenia Lagrange’a):

(10.2.1) Jeżeli pochodna funkcji jest w pewnym przedziale dodatnia, to funkcja jest w t)ⁿ‘ przedziale rosnąca.

(10.2.2) Jeżeli pochodna funkcji jest w pewnym przedziale ujemna, to funkcja jest w W¹*¹przedziale malejąca.

(10.2.3) Jeżeli pochodna funkcji jest w każdym punkcie pewnego przedziału równa td to funkcja ma w tym przedziale wartość stałą.

Mówimy, że funkcja y=f (x) ma w punkcie x₀ maksimum lokalne (minimum jeżeli istnieje takie otoczenie punktu x₀, że dla wszystkich punktów tego otoczenia

chodzi nierówność

f(x) <f(x₀) (/(*)>/(*„)).

\fiksi^ma i minima funkcji noszą wspólną nazwę ekstremów funkcji.

Wyznaczenie ekstremum funkcji (maksimum lub minimum) opiera się na następujących

twierdzeniach:

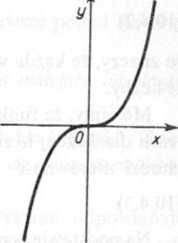
Rys. 10.3

^10 2.4) Twierdzenie Fermata. Jeżeli funkcja różniczkowalna _v przedziale osiąga w pewnym punkcie wewnętrznym x=x₀ tego przedziału ekstremum lokalne, to pochodna w tym punkcie f'{x„) równa się zeru.

Twierdzenie odwrotne nie jest prawdziwe. Na przykład funkcja y=x³ ma pochodną y' = 3x², która jest równa zeru <ji_a x=0; w punkcie tym funkcja nie posiada ekstremum (rys 10.3).

(10.2.5) Jeżeli pierwsza pochodna f'{x) dla x<x₀ jest ujemna (dodatnia), dla x=x₀ jest równa zeru, a dla x>x₀ jest dodatnia {ujemna), co wyrażamy często krócej, mówiąc: pochodna przy przejściu zmiennej x przez punkt x₀ zmienia znak z ujemnego na dodatni (z dodatniego na ujemny), to funkcja y=f(x) osiąga ekstremum {minimum w pierwszym, a maksimum w drugim przypadku).

§ 10.3. PUNKTY PRZEGIĘCIA

Punktem przegięcia wykresu funkcji y =/(*), gdy funkcja f{x) ma drugą pochodną ^C13głą, nazywamy taki jej punkt, w którym styczna do krzywej przechodzi z jednej strony kzywej na drugą.

Na przykład początek układu współrzędnych jest punktem przegięcia krzywej y=x³; ⁰⁵ Ox jest styczna do krzywej w punkcie (0, 0) i jednocześnie przecina krzywą w punkcie %zności (rys. 10.3).

Punkty przegięcia wyznaczamy za pomocą następujących twierdzeń:

M-3.1) Jeżeli funkcja y=f{x) ma drugą pochodną ciągłą, to w punktach przegięcia okresu funkcji druga pochodna f"{x) jest równa zeru.

twierdzenie odwrotne nie jest prawdziwe. Na przykład druga pochodna dla ftmkcji jest równa zeru dla x = 0, a wykres funkcji nie ma jednak punktu przegięcia (ma w tym ^pu«kcie minimum).

n_a

odnt

.t^-2) Jeżeli druga pochodna f"{x) dla x<x₀ jest ujemna {dodatnia), dla x = x₀ jest

zeru, a dla x>x₀ jest dodatnia {ujemna), co wyrażamy krócej, mówiąc: druga po-n_Q ^{na prz}P przejściu przez punkt x₀ zmienia znak z ujemnego na dodatni (z dodatniego ^uJemny), to wykres funkcji y=f{x) ma punkt przegięcia w punkcie x₀.