116 117 (4)

116

Przestrzenie euklidcsowe

3. (aź, y) = 3 (azij y; - 2(crn ) y₂ - 2(q'X₂}»i +4 {orz₂)y_a= ar(3i|yi - 2xjy₂ - 2r₂yi + 4r₂y2)

= n(x, y).

Sprawdzamy warunek 4. Mamy (x, i) = Zz] - 4xir₂ + 4x2- Jest to trójmian kwadratowy zmiennej i\, dla którego A = -32 (z₂)² ^ 0 Stąd wynika, że (i x) ^ 0. Warunek 5. jest także spełniony, bowiem oczywiście (0 0) = 0 Jeżeli natomiast (z. x) = 0, to rozważany poprzednio trójmian kwadratowy ma pierwiastek i A = 0. Stąd x₂ — 0 oraz x ] — 0, zatem z — 0.

b) Niech p, <7 r e /2i [jc] oraz a € R Podobnie jak poprzednio mamy

1 (p.<7> = P(0fl(l) + 2P(2)«(2)= 7(l)p(l)+2ę(2)p(2) = (q,p)

2. (p + q, r) = *>(!)+ ?(1)) K¹) + 2(p(2) -+ g(2)) r(2)

= (p(l)r{l) + 2p(2)r(2)) + (qr(l)r(l) + 29(2)r(2))

= (P. ) + (. ^r).

3. (ap,9) = (»p(l))ę(l) + 2(ap(2))7(2) = «(p(J)?(l) + 2j>(2)*(2))

= a(p. 9),

4 (P,P) = P²(l) + 2p²(2)^0_!

5 (o, 0) = 0, a 2 warunku (p, p) = 0 wynika żc p(l) = p(2) = 0.

Funkcja p jest wielomianem stopnia 1 lub funkcją stałą. Zerowanie się tej funkcji w punktach 1 = 1 i r = 2 oznacza, żc p(x) = 0.

• Przykład 12.2

Uzasadnić, ze podane funkcje (•»•) nie są iloczynami skalarnymi we wskazanych przestrzeniach liniowych:

a) (5, y) = 5riy\ - 3z_:y₂ - 3r₂J/i + ywi dla x = (xi, x₂), y = (yi,y₂) € #²;

b) (5, y) = [ri *2 *3]

2 1 3 -1 1 0

3 0 1

r *

dla 1 = (z_lt x₂, x₃) y = (yi y₂, y₃) 6 R*_tO (P. = p(0)ę(0) + p(i)ę(l) dla p, q 6 IŁjfz].

Rozwiązanie

a) Funkcja (•,•) nie spełnia warunku 4. (patrz rozwiązanie Przykładu 12.1) definicji iloczynu s.<alarnego. Traktując bowiem wyrażenie (z, z) = 5xJ-6xj z₂ + x₂ jako trójmian kwadratowy zmiennej x_x otrzymujemy związek A = 16r₂ ^ 0. Możliwa jest więc sytuacja, że (x, z) < 0 np. dla z = f-,lV Dodatkowo można jeszcze zauważyć, że istnieje niezerowy wektor, np z — (1,1), dla którego (z, z) = 0. To oznacza, że również warunek 5. definicji iloczynu skalarnego nie jest spełniony.

b) W tym przykładzie warunek 1. definicji iloczynu skalarnego nie jest spełniony. Macierz

definiująca funkcję ( ) nic jest symetryczna i łatwo wskazać dwa wektory, np. x =

(1,0 0), y = (0,1,0), dla których (x, y) = 1 ^ — 1 = (y, x).

c) Załóżmy, że dla pewnego wielomianu p € -ft₂[x^ zachodzi związek (p. p) = 0. To oznacza, że p²(0) -f p²(l) = 0, a zatem p(0) = p(l) = 0. Łatwo wskazać niezerowy

Dwunasty tydzień - pizykłady 117

wielomian p stopnia ^ 2 spełniający otrzymaną zależność, np. p(x) = x(x— 1). Warunek 5. definicji iloczynu skalarnego me jest więc spełniony

• Przykład 12.3

W przestrzeni euklidcsowcj E^A

a) obliczyć, normę wektora (1, —2,3, —4);

b) zbadać ortcgonalność wektorów (2, —3,1,—1), (6.1,— 2,7);

c) obliczyć kąt miedzy wektorami (1,2,1,—2), (—2,1 0,1);

d) znaleźć wszystkie wektory ortogonalne do wektora (1,0,1,0) i wskazać jeden taki wektor o normie równej 3;

c| podać przykład wektora unormowanego tworzącego z wektorem (1,1 —1,0)

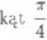
Rozwiązanie

a) Niech i = (1, — 2, 3, — 4). Wówczas

|i| = sj(i,x) = V'l² + (-2)’ + 3² + (—4)² = y/30.

b) Oznaczmy podane wekLory odpowiednio przez Z, y. Mamy (z, y) = 0. zatem wektory te są ortogonalne.

c) Dla podanych wektorów z, y mamy

cos i (z, y) =

(g.y) ₌ ~2

1*1 liżl y/iÓy/S

yTs

15 '

czyli $ {x,y) = arccos ( J

d) Dowolny wektor X = (a,ł>,c,d) € E^ł ortogonalny dodanego wektora y spełnia związek [z, y) = u + c = 0. Stąd wynika, że x = (a b, -a.d), gdzie a,b,d£ R Wszystkie wektory o tej własności tworzą więc przestrzeń Umową Un {(1,0, — 1, 0), (0, 1,0, 0), (0, 0,0. 1)}. Wektor o normie równej 3 należący do tej przestrzeni spełnia dodatkowo warunek 2a² + b² + d⁷ = 9. Przykładem takiego wektora jest Zo = (2,1,—2,0).

c) Niech x = (u,b,c,d) będzie szukanym wektorem, y = (1,1,—1,0). Wówczas mamy a² 4- b^d + c² + d^A = 1 oraz

cos 4 {z, y) =

a + b — c

~7T~

s/2

Stąd wynika, że a -f- b

— - y/d, zaś d = y/1 — a⁴4

c = i\/6. Przykładowo można przyjąć, że a — b — i\/6, c =

2 o

b⁷ — c² — i\/7 Ostatecznie X = ( iv6, ^ ^6, — - V6, i .

• Przykład 12.4

Obliczyć kąty między wektorami p₃ = 2 — 4x, ę₀ = x - 2 w przestrzeni eukiideso-wej 12i[x) 7. podanymi iloczynami skalarnymi:

116 117 (4)

116 117 (4)

= (P. *) + (*. r).

2 1 3 -1 1 0

3 0 1

r *

Dwunasty tydzień - pizykłady 117

• Przykład 12.3

(g.y) = ~2

yTs

• Przykład 12.4

= (P. ) + (. ^r).

(g.y) ₌ ~2